Jams倒酒(pour)
1s,256MB
题目描述
Jams是一家酒吧的老板,他的酒吧提供2种体积的啤酒,a ml 和 b ml,分别使用容积为a ml 和 b ml的酒杯来装载。
酒吧的生意并不好。Jams发现酒鬼们都很穷,不像他那么土豪。有时,他们会因为负担不起a ml 或者 b ml酒的消费,而不得不离去。因此,Jams决定出手第三种体积的啤酒(较小体积的啤酒)。
Jams只有两种杯子,容积分别为 a ml 和 b ml,而且啤酒杯是没有刻度的。他只能通过两种杯子和酒桶间的互相倾倒来得到新的体积的酒。
倒酒步骤为:
(1) 规定a>=b
(2) 酒桶容积无限,酒桶中酒体积无限大。
(3) 只能包含三种可能的倒酒操作:
1、 将酒桶中的酒倒入容积为b ml的酒杯中;
2、 将容积为a ml的酒杯中的酒倒入酒桶;
3、 将容积为b ml的酒杯中的酒倒入容积为 a ml的酒杯中。
(4) 每次倒酒必须把杯子倒满或者把被倾倒的杯子倒空。
Jams希望通过若干次倾倒得到容积为 a ml酒杯中剩下的就体积尽可能小,他请求你帮助他设计倾倒方案。
输入
两个整数a,b(0<b<=a<=10^9)
输出
第一行一个整数,表示可以得到的最小体积的酒。
第二行两个整数Pa和Pb(中间用一个空格分开),分别表示从体积为a ml的酒杯中到处酒的次数和将酒倒入体积为b ml的酒杯的次数。
若有多种可能的Pa,Pb满足要求,那么请输出Pa最小的。若Pa最小的时候有多个Pb,那么输出Pb最小的。
样例输入
5 3
样例输出
1
1 2
提示&约定
倾倒方案为: 1、 桶->B; 2、 B->A; 3、 桶->B; 4、 B->A; 5、 A->桶; 6、 B->A;
对于20%的数据,pa,pb总和不超过5 对于60%的数据,pa<=10^8 对于100%的数据,0<b<=a<=10^9
solution
对于一个a>b

每次都是把B倒满,把B倒入A,这时候B不一定倒完,但A满了,把A倒掉,把B中剩下的倒入A……这样循环下去。能取到酒的量为\(-ax+by\),所以能取到的最小值就是\(gcd(a,b)\)
我们要求\(-ax+by=gcd(a,b)\),所以用exgcd先求出一组x,y的解,然后判断x,y是否可以变小,或者y小于0,那么x变小,y变大。
code
#include<bits/stdc++.h>
#define ll long long
#define fsb(a,b,c) for(ll a=b;a<=(c);a++)
#define fbs(a,b,c) fro(ll a=b;a>=(c);a--)
using namespace std;
ll a,b,x,y,ans,tx,ty;
template<typename qw>inline void rll(qw &x){
qw f=1;x=0;char c=getchar();
while(!isdigit(c))f=c=='-'?-1:f,c=getchar();
while(isdigit(c))x=x*10+c-'0',c=getchar();
x*=f;
}
inline ll exgcd(ll a,ll b,ll &x,ll &y){
if (b==0) {
x=1;y=0;
return a;
}
ll ans=exgcd(b,a%b,x,y);
ll t=x;x=y;
y=t-a/b*y;
return ans;
}
int main(){
freopen("pour.in","r",stdin);freopen("pour.out","w",stdout);
rll(a);rll(b);ans=exgcd(a,b,x,y);
printf("%lld\n",ans);x*=-1;tx=b/ans;ty=a/ans;
if(x<0){
ll t=(0-x)/tx+((0-x)%tx!=0?1:0);
x+=t*tx;y+=t*ty;
}
if(y<0){
ll t=(0-y)/ty+((0-y)%ty!=0?1:0);
x+=t*tx;y+=t*ty;
}
printf("%lld %lld\n",x,y);
return 0;
}
土豪聪要请客(stol)
1s,256MB
题目描述
众所周知,聪哥(ndsf)是个土豪,不过你们不知道的是他的MZ和他的RMB一样滴多…… 某天土豪聪又赚了10^10000e的RMB,他比较开心,于是准备请客。他在自己在XX星上的别墅里面大摆酒席,想要邀请尽可能多的MZ来参加他的宴会。他将会同MZ一起坐在一个巨大的长方形桌子上。这个桌子能坐下的人数等于他的边长。聪哥要求他的桌子能够放进他的别墅,并且桌子的边必须与别墅的边界平行。给定别墅的平面图,请你求出聪哥最多可以请多少个MZ。
输入
第一行n,m。表示别墅的长宽 下面n行,每行M个字符,表示一个方块是空的('.')或是被占用了('X')。 聪哥只要他的桌子放在别墅里,并且桌子不能占用任何一个已经占用了的方块。
输出
一个数,表示聪哥最多可以请几个Maze。
样例输入1
2 2
..
..
样例输出1
7
样例输入2
4 4
X.XX
X..X
..X.
..XX
样例输出2
9
提示&约定
对于60%的数据,n,m<=100 对于100%的数据,n,m<=400
solution
枚举m上的边长范围,然后对n跑最大连续子段和
code
#include<bits/stdc++.h>
#define N 410
#define max(a,b) ((a)>(b)?(a):(b))
#define fsb(a,b,c) for(register int a=b;a<=(c);a++)
#define fbs(a,b,c) fro(register int a=b;a>=(c);a--)
using namespace std;
int a[N][N],n,m,ans=0,f[N];
char s[N];
template<typename qw>inline void rll(qw &x){
qw f=1;x=0;char c=getchar();
while(!isdigit(c))f=c=='-'?-1:f,c=getchar();
while(isdigit(c))x=x*10+c-'0',c=getchar();
x*=f;
}
inline int check(int i1,int i2,int j1,int j2){
i1--;j1--;
return a[i2][j2]-a[i1][j2]-a[i2][j1]+a[i1][j1]==0;
}
inline int calc(int l,int r){
return (l+r)*2-1;
}
int main(){
freopen("stol.in","r",stdin);freopen("stol.ans","w",stdout);
rll(n);rll(m);memset(a,0,sizeof(a));
fsb(i,1,n){
scanf("%s",s+1);
fsb(j,1,m)a[i][j]=(s[j]=='X'?1:0)+a[i-1][j]+a[i][j-1]-a[i-1][j-1];
}
// fsb(i,1,n){fsb(j,1,m)printf("%3d",a[i][j]);puts("");}
fsb(i,1,m)fsb(j,i,m){
memset(f,255,sizeof(f));
fsb(k,1,n){
if(!check(k,k,i,j))continue;
f[k]=1+max(0,f[k-1]);
ans=max(calc(j-i+1,f[k]),ans);
}
}
printf("%d\n",ans);
return 0;
}
最强大脑(zhber)
5s,256MB
问题描述
zhb国是一个传说中的国度,国家的居民叫做最强(chang)大脑(diao)。Zhb国是一个N×M的矩形方阵,每个格子代表一个街区。 然而zhb国是没有交通工具的。居民大脑(diao)们完全靠地面的弹射装置来移动。 每个街区都装有弹射装置。使用弹射装置是需要支付一定费用的。而且每个弹射装置都有自己的弹射能力。 我们设第i行第j列的弹射装置有Aij的费用和Bij的弹射能力。并规定有相邻边的格子间距离是1。那么,任何居民大脑(diao)都只需要在(i,j)支付Aij的费用就可以任意选择弹到距离不超过Bij的位置了。如下图
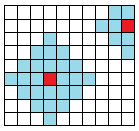
(从红色街区交费以后可以跳到周围的任意蓝色街区。)
现在的问题很简单。有三个居民,她们分别是zhb的maze,分别叫做X,Y,Z。现在她们决定聚在一起玩找zhb玩(….),于是想往其中一人的位置集合。但由于zhb太抠门了,不给报销路费,所以告诉你3个maze的坐标,求往哪里集合大家需要花的费用总和最低。 Zhb:如果你完美解决了这个问题,就授予你“最强(chang)大脑(diao)”称号。
输入
输入的第一行包含两个整数N和M,分别表示行数和列数。 接下来是2个N×M的自然数矩阵,为Bij和Aij 最后一行六个数,分别代表X,Y,Z所在地的行号和列号。
输出
第一行输出一个字符X、Y或者Z。表示最优集合地点。 第二行输出一个整数,表示最小费用。 如果无法集合,只输出一行NO
样例输入
4 4
0 0 0 0
1 2 2 0
0 2 2 1
0 0 0 0
5 5 5 5
5 5 5 5
5 5 5 5
5 5 5 5
2 1 3 4 2 2
样例输出
Z
15
提示&约定
20% N, M ≤ 10; Bij ≤ 20 40% N, M ≤ 100; Bij ≤ 20 100% 1 ≤ N, M ≤ 150; 0 ≤ Bij ≤ 109; 0 ≤ Aij ≤ 1000
solution
跑3遍堆优化dijk
code
#include<bits/stdc++.h>
#define N 160
#define ll long long
#define mem(a,b) memset(a,b,sizeof(a))
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define INF 99999999
#define abs(a) ((a)>0?(a):(-(a)))
#define fsb(a,b,c) for(register int a=b;a<=(c);a++)
#define fbs(a,b,c) for(register int a=b;a>=(c);a--)
using namespace std;
int n,m,a[N][N],b[N][N],sz;
int di[N][N],po[N][N],X[N][N],Y[N][N],Z[N][N],xx,xy,yx,yy,zx,zy,vi[N][N];
struct node{
int x,y;
}s[N*N];
template<typename qw>inline void rll(qw &x){
qw f=1;x=0;char c=getchar();
while(!isdigit(c))f=c=='-'?-1:f,c=getchar();
while(isdigit(c))x=x*10+c-'0',c=getchar();
x*=f;
}
inline void sup(int u){
int son=u;
while(son>1&&(di[s[son].x][s[son].y]<di[s[son>>1].x][s[son>>1].y])){
swap(po[s[son].x][s[son].y],po[s[son>>1].x][s[son>>1].y]);
swap(s[son],s[son>>1]);
son>>=1;
}
}
inline void sdown(int u){
int fa=u,son;
while(fa*2<=sz){
son=fa*2;son+=(son+1<=sz&&di[s[son+1].x][s[son+1].y]<di[s[son].x][s[son].y])?1:0;
if(di[s[son].x][s[son].y]<di[s[fa].x][s[fa].y]){
swap(po[s[fa].x][s[fa].y],po[s[son].x][s[son].y]);
swap(s[son],s[fa]);
fa=son;
}else break;
}
}
inline void spush(int x,int y){
s[++sz]=(node){x,y};po[x][y]=sz;
sup(sz);
}
inline void spop(){
po[s[1].x][s[1].y]=0;if(sz==1){sz=0;return;}
s[1]=s[sz--];po[s[1].x][s[1].y]=1;sdown(1);
}
int main(){
freopen("fly.in","r",stdin);freopen("fly.out","w",stdout);
rll(n);rll(m);
fsb(i,1,n)fsb(j,1,m)rll(b[i][j]);
fsb(i,1,n)fsb(j,1,m)rll(a[i][j]);
rll(xx);rll(xy);rll(yx);rll(yy);rll(zx);rll(zy);
//work X
mem(di,60);mem(po,0);mem(vi,0);
sz=0;di[xx][xy]=0;spush(xx,xy);
while(sz>0&&((!vi[yx][yy])||(!vi[zx][zy]))){
int x=s[1].x,y=s[1].y;spop();vi[x][y]=1;
// printf("%10d %d\n",x,y);
fsb(i,max(x-b[x][y],1),min(x+b[x][y],n))
fsb(j,max(y-(b[x][y]-abs(i-x)),1),min(y+(b[x][y]-abs(i-x)),m)){
if(di[i][j]<=di[x][y]+a[x][y])continue;
di[i][j]=di[x][y]+a[x][y];
if(po[i][j]==0)spush(i,j);
else sup(po[i][j]);
}
}
X[xx][xy]=di[xx][xy];X[yx][yy]=di[yx][yy];X[zx][zy]=di[zx][zy];
//work Y
mem(di,60);mem(po,0);mem(vi,0);
sz=0;di[yx][yy]=0;spush(yx,yy);
while(sz>0&&((!vi[xx][xy])||(!vi[zx][zy]))){
int x=s[1].x,y=s[1].y;spop();vi[x][y]=1;
// printf("%10d %d\n",x,y);
fsb(i,max(x-b[x][y],1),min(x+b[x][y],n))
fsb(j,max(y-(b[x][y]-abs(i-x)),1),min(y+(b[x][y]-abs(i-x)),m)){
if(di[i][j]<=di[x][y]+a[x][y])continue;
di[i][j]=di[x][y]+a[x][y];
if(po[i][j]==0)spush(i,j);
else sup(po[i][j]);
}
}
Y[xx][xy]=di[xx][xy];Y[yx][yy]=di[yx][yy];Y[zx][zy]=di[zx][zy];
//work Z
mem(di,60);mem(po,0);mem(vi,0);
sz=0;di[zx][zy]=0;spush(zx,zy);
while(sz>0&&((!vi[yx][yy])||(!vi[xx][xy]))){
int x=s[1].x,y=s[1].y;spop();vi[x][y]=1;
// printf("%10d %d\n",x,y);
fsb(i,max(x-b[x][y],1),min(x+b[x][y],n))
fsb(j,max(y-(b[x][y]-abs(i-x)),1),min(y+(b[x][y]-abs(i-x)),m)){
if(di[i][j]<=di[x][y]+a[x][y])continue;
di[i][j]=di[x][y]+a[x][y];
if(po[i][j]==0)spush(i,j);
else sup(po[i][j]);
}
}
Z[xx][xy]=di[xx][xy];Z[yx][yy]=di[yx][yy];Z[zx][zy]=di[zx][zy];
int ans=-1,ans1=INF;
if(Y[xx][xy]+Z[xx][xy]<ans1){
ans1=Y[xx][xy]+Z[xx][xy];
ans=1;
}
if(X[yx][yy]+Z[yx][yy]<ans1){
ans1=X[yx][yy]+Z[yx][yy];
ans=2;
}
if(X[zx][zy]+Y[zx][zy]<ans1){
ans1=X[zx][zy]+Y[zx][zy];
ans=3;
}
if(ans==-1){
puts("NO");return 0;
}
puts(ans==1?"X":(ans==2?"Y":"Z"));printf("%d\n",ans1);
return 0;
}